Omo dėsnis visai grandinei ir grandinės atkarpai: formulės parinktys, aprašymas ir paaiškinimas

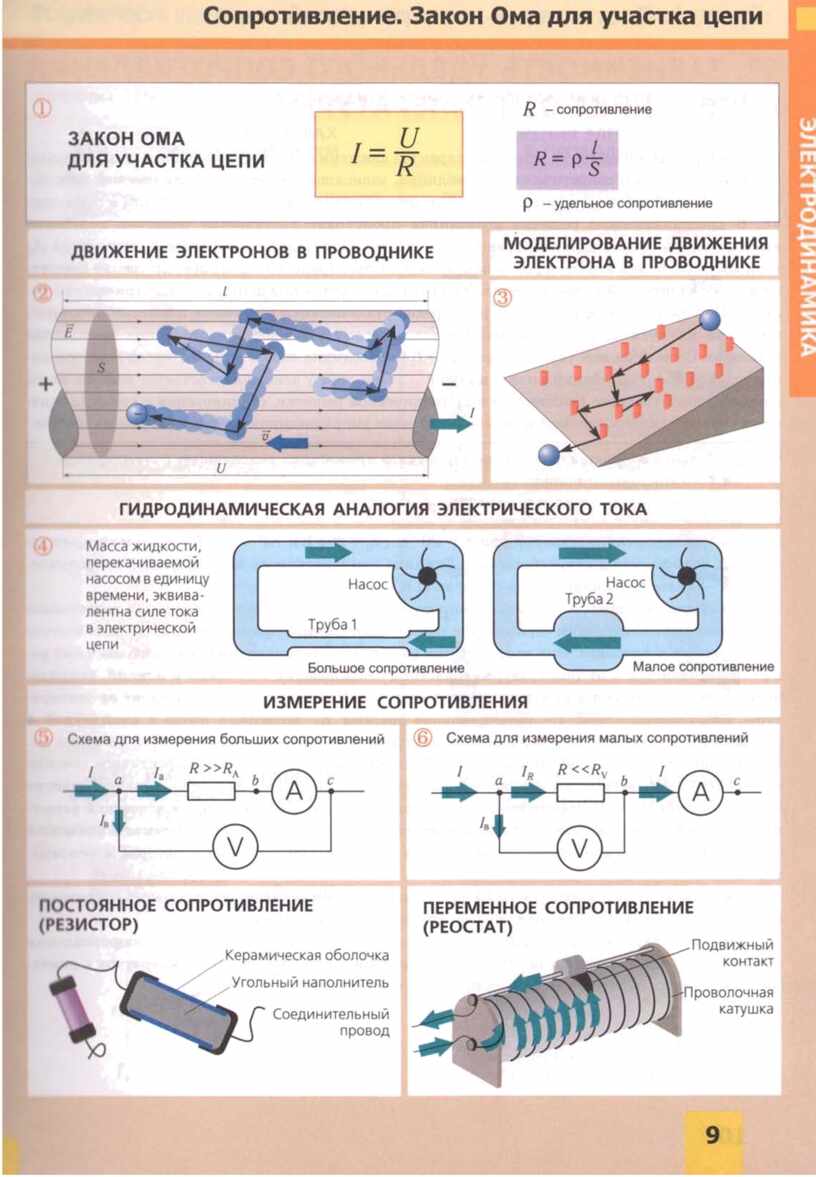
Uždarai grandinei

Uždara grandinė reiškia uždarą elektros jungtį, per kurią cirkuliuoja srovė. Kai laidai jungiasi vienas su kitu ir užbaigia grandinę taip, kad aš einu nuo vieno apskritimo galo iki kito, tai bus uždara grandinė.

EMF (E) – žymimas ir matuojamas voltais ir nurodo įtampą, kurią sukuria baterija arba magnetinė jėga pagal Faradėjaus dėsnį, kuris teigia, kad laikui bėgant kintantis magnetinis laukas sukels elektros srovę.

Tada: E = IR + Ir

E \u003d I (R + r)

I \u003d E / (R + r)

Kur: r yra srovės šaltinio varža.

Ši išraiška žinoma kaip Omo uždarojo ciklo grandinių dėsnis.

Heterogeninė grandinė

Atskira sekcija ir visa elektros grandinė

Omo dėsnį, taikomą sekcijai arba visai grandinei, galima apsvarstyti dviem skaičiavimo variantais:

• Atskiras trumpas skyrius. Tai dalis grandinės be EML šaltinio.
• Visa grandinė, susidedanti iš vienos ar kelių sekcijų. Tai taip pat apima EML šaltinį su savo vidine varža.

Elektros grandinės srovės atkarpos apskaičiavimas

Šiuo atveju taikoma pagrindinė formulė I \u003d U / R, kurioje I yra srovės stiprumas, U yra įtampa, R yra varža. Pagal jį galima suformuluoti visuotinai priimtą Ohmo dėsnio aiškinimą:

Ši formulė yra daugelio kitų formulių, pateiktų grafinio dizaino vadinamojoje „ramunėlėje“, pagrindas. P sektoriuje - nustatoma galia, I, U ir R sektoriuose - atliekami veiksmai, susiję su srovės stiprumu, įtampa ir varža.

Kiekviena išraiška - tiek pagrindinė, tiek papildoma - leidžia apskaičiuoti tikslius elementų, skirtų naudoti grandinėje, parametrus.

Specialistai, dirbantys su elektros grandinėmis, atlieka greitą bet kurio parametro nustatymą trikampio metodu, parodytu paveikslėlyje.

Skaičiuojant reikėtų atsižvelgti į sekcijos elementus jungiančių laidininkų varžą. Kadangi jie pagaminti iš skirtingų medžiagų, šis parametras kiekvienu atveju skirsis.Jei reikia sudaryti visą grandinę, pagrindinė formulė papildoma įtampos šaltinio, pavyzdžiui, akumuliatoriaus, parametrais.

Skaičiavimo parinktis visai grandinei

Visa grandinė susideda iš atskirų sekcijų, sujungtų į vieną visumą kartu su įtampos šaltiniu (EMF). Taigi, esamą sekcijų varžą papildo prijungto šaltinio vidinė varža. Todėl pagrindinis anksčiau aptartas aiškinimas bus toks: I = U / (R + r). Čia jau pridėtas EML šaltinio varžos indikatorius (r).

Grynosios fizikos požiūriu šis rodiklis laikomas labai maža reikšme. Tačiau praktikoje, skaičiuodami sudėtingas grandines ir grandines, specialistai yra priversti į tai atsižvelgti, nes papildomas pasipriešinimas turi įtakos darbo tikslumui. Be to, kiekvieno šaltinio struktūra yra labai nevienalytė, todėl kai kuriais atvejais atsparumas gali būti išreikštas gana dideliais rodikliais.

Aukščiau pateikti skaičiavimai atliekami nuolatinės srovės grandinių atžvilgiu. Veiksmai ir skaičiavimai su kintama srove atliekami pagal kitą schemą.

Įstatymo poveikis kintamajam

Esant kintamajai srovei, grandinės varža bus vadinamoji varža, kurią sudaro aktyvioji varža ir reaktyvioji varžinė apkrova. Taip yra dėl elementų, turinčių indukcines savybes ir sinusinės srovės vertės. Įtampa taip pat yra kintamoji, veikianti pagal jos perjungimo dėsnius.

Todėl Omo dėsnio kintamosios srovės grandinės konstrukcija apskaičiuojama atsižvelgiant į specifinius efektus: srovės stiprumo vedimą arba atsilikimą nuo įtampos, taip pat aktyviosios ir reaktyviosios galios buvimą.Savo ruožtu reaktyvumas apima indukcinius arba talpinius komponentus.

Visi šie reiškiniai atitiks formulę Z \u003d U / I arba Z \u003d R + J * (XL - XC), kurioje Z yra varža; R - aktyvi apkrova; XL, XC - indukcinės ir talpinės apkrovos; J yra pataisos koeficientas.

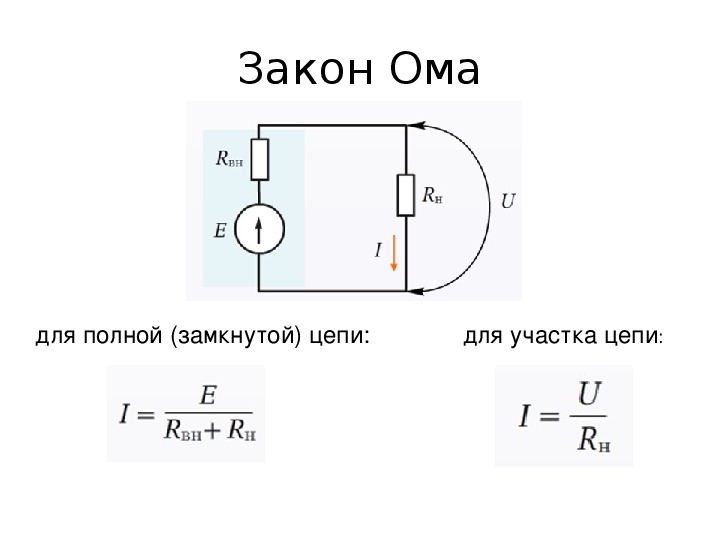
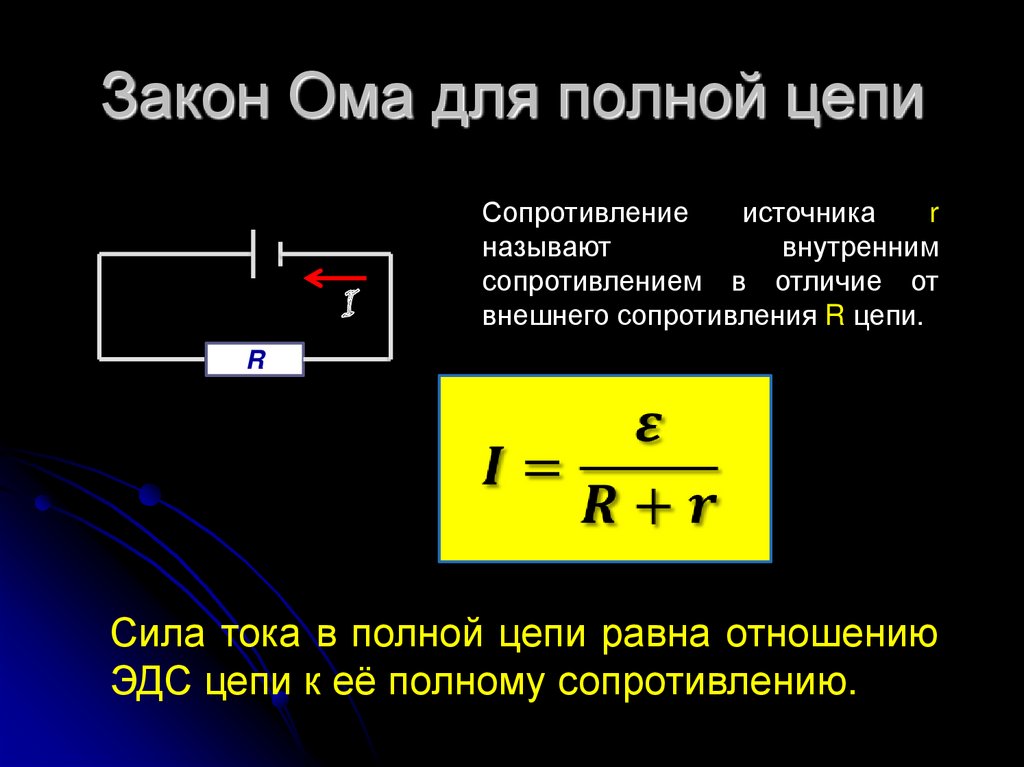
EML šaltinis pilnoje grandinėje

Kad uždaroje grandinėje atsirastų elektros srovė, šioje grandinėje turi būti bent vienas specialus elementas, kuriame vyks krūvių perkėlimo tarp jos polių darbas. Jėgos, pernešančios krūvius šio elemento viduje, veikia prieš elektrinį lauką, o tai reiškia, kad jų pobūdis turi skirtis nuo elektrinio. Todėl tokios jėgos vadinamos trečiosiomis šalimis.

Ryžiai. 1. Išorinės jėgos fizikoje.

Elektros grandinės elementas, kuriame išorinės jėgos perduoda krūvius prieš elektrinio lauko veikimą, vadinamas srovės šaltiniu. Pagrindinė jo charakteristika yra išorinių jėgų dydis. Jai apibūdinti įvedamas specialus matas - Elektromotorinė jėga (EMF), ji žymima raide $\mathscr{E}$.

Srovės šaltinio EML vertė yra lygi išorinių jėgų, skirtų krūviui perduoti, ir šio krūvio vertės santykiui:

$$\mathscr{E}={A_{st}\daugiau nei q}$$

Kadangi EML reikšmė labai artima elektros įtampos reikšmei (prisiminkime, įtampa yra krūvį pernešančio elektrinio lauko darbo ir šio krūvio vertės santykis), tai EML, kaip ir įtampa, matuojamas Voltai:

$$1B={J\overCl}$$

Antra pagal svarbą tikrojo srovės šaltinio elektrinė charakteristika yra jo vidinė varža.Kai krūviai perduodami tarp gnybtų, jie sąveikauja su EML šaltinio medžiaga, todėl elektros srovės šaltinis taip pat turi tam tikrą pasipriešinimą. Vidinė varža, kaip ir įprasta varža, matuojama omais, tačiau žymima maža lotyniška raide $r$.

Ryžiai. 2. Srovės šaltinių pavyzdžiai.

R - elektrinė varža

Atsparumas yra įtampos atvirkštinis dydis ir gali būti lyginamas su kūno judėjimo prieš judėjimą poveikiu tekančiame vandenyje. R vienetas yra Om, kuris žymimas didžiąja graikiška raide Omega.

Atsparumo koeficientas (1/R) yra žinomas kaip laidumas, kuris matuoja objekto gebėjimą atlikti krūvį, išreikštą Siemens vienetais.

Naudojamas geometriškai nepriklausomas dydis vadinamas varža ir paprastai žymimas graikišku simboliu r.

Papildoma informacija. Omo dėsnis padeda nustatyti tris svarbius elektros tinklo veikimo rodiklius, kurie supaprastina galios skaičiavimą. Jis netaikomas vienpusiams tinklams su tokiais elementais kaip diodas, tranzistorius ir pan. Taip pat tai netaikoma nelinijiniams elementams, kurių pavyzdžiai yra tiristoriai, nes šių elementų varžos vertė kinta esant skirtingai įtampai ir srovei.

Esant aukštesniems dažniams, paskirstytas elgesys tampa dominuojančiu. Tas pats atsitinka su labai ilgomis elektros linijomis. Net esant 60 Hz dažniui, labai ilga perdavimo linija, pavyzdžiui, 30 km, yra paskirstyta. Pagrindinė priežastis yra ta, kad efektyvūs elektros signalai, sklindantys grandinėse, yra elektromagnetinės bangos, o ne voltai ir amperai, kuriuos užkrečia elektromagnetinė banga.Laidininkai tiesiog veikia kaip bangų vadovai. Taigi, pavyzdžiui, bendraašis kabelis parodys Z = 75 omas, net jei jo nuolatinės srovės varža yra nereikšminga.

Omo dėsnis yra pagrindinis elektros inžinerijos dėsnis. Jis turi daug praktinių pritaikymų visose elektros grandinėse ir elektroniniuose komponentuose.

Dažniausi Ohmo dėsnio taikymo pavyzdžiai:

1. Energija tiekiama į elektrinį šildytuvą. Atsižvelgiant į šildytuvo gyvatuko varžą ir taikomą įtampą, galima apskaičiuoti į šildytuvą tiekiamą galią.
2. Saugiklių pasirinkimas. Tai apsaugos komponentai, nuosekliai sujungti su elektroniniais prietaisais. Saugikliai/CB vardiniai amperais. Dabartinis saugiklis apskaičiuojamas pagal Ohmo dėsnį.
3. Elektroninių prietaisų projektavimas. Elektroniniams prietaisams, tokiems kaip nešiojamieji kompiuteriai ir mobilieji telefonai, reikalingas tam tikros srovės srovės tiekimas. Įprastoms mobiliųjų telefonų baterijoms reikia 0,7-1 A. Šiuose komponentuose tekančios srovės greičiui valdyti naudojamas rezistorius. Omo dėsnis naudojamas apskaičiuoti vardinę srovę tipinėje grandinėje.

Kadaise Ohmo išvados tapo naujų tyrimų elektros energijos srityje katalizatoriumi, o šiandien jos neprarado savo reikšmės, nes jomis remiasi šiuolaikinė elektrotechnika. 1841 metais Om buvo apdovanotas aukščiausiu Karališkosios draugijos apdovanojimu – Copley medaliu, o terminas „Om“ buvo pripažintas pasipriešinimo vienetu jau 1872 m.

Nevienoda nuolatinės srovės grandinės dalis

Heterogeninė struktūra turi tokią grandinės sekciją, kurioje, be laidininkų ir elementų, yra ir srovės šaltinis. Skaičiuojant bendrą srovės stiprumą šioje srityje, reikia atsižvelgti į jo EMF.

Yra formulė, apibrėžianti pagrindinius heterogeninės aikštelės parametrus ir procesus: q = q0 x n x V. Jos rodikliai apibūdinami taip:

• Judėdami krūviams (q) jie įgauna tam tikrą tankį. Jo veikimas priklauso nuo srovės stiprumo ir laidininko skerspjūvio ploto (S).
• Tam tikros koncentracijos (n) sąlygomis galima tiksliai nurodyti vienetinių įkrovų skaičių (q0), kurie buvo perkelti per vieną laikotarpį.
• Skaičiavimui laidininkas sąlyginai laikomas cilindrine sekcija, kurios tūris yra (V).

Prijungus laidininką prie akumuliatoriaus, pastarasis po kurio laiko išsikraus. Tai yra, elektronų judėjimas palaipsniui lėtėja ir galiausiai visiškai sustoja. Tai palengvina laidininko molekulinė gardelė, kuri neutralizuoja elektronų susidūrimą tarpusavyje ir kitus veiksnius. Norint įveikti tokį pasipriešinimą, reikia papildomai panaudoti tam tikras trečiųjų šalių jėgas.

Skaičiuojant šios jėgos pridedamos prie Kulono jėgų. Be to, norint perkelti vienetinį krūvį q iš 1 taško į 2, reikės atlikti darbą A1-2 arba tiesiog A12. Šiuo tikslu sukuriamas potencialų skirtumas (ϕ1 - ϕ2). Veikiant nuolatinės srovės šaltiniui, atsiranda EML, perkeldamas krūvius grandinėje. Bendro įtempio dydį sudarys visos aukščiau nurodytos jėgos.

Atliekant skaičiavimus reikia atsižvelgti į prijungimo prie nuolatinės srovės maitinimo poliškumą. Pakeitus gnybtus, pasikeis ir EMF, pagreitindamas arba sulėtindamas krūvių judėjimą.

Nuoseklus ir lygiagretus elementų sujungimas

Elektros grandinės elementams (grandinės atkarpai) būdingas momentas yra nuosekli arba lygiagreti jungtis.

Atitinkamai, kiekvieną jungties tipą lydi skirtingas srovės srauto ir įtampos tiekimo pobūdis. Atsižvelgiant į tai, Ohmo įstatymas taip pat taikomas įvairiais būdais, atsižvelgiant į elementų įtraukimo parinktį.

Serijiniu būdu sujungtų varžinių elementų grandinė

Kalbant apie nuoseklųjį sujungimą (schemos atkarpą su dviem komponentais), vartojama formuluotė:

• aš = aš₁ = aš₂ ;
• U = U₁ + U₂ ;
• R=R₁ + R₂

Ši formuluotė aiškiai parodo, kad nepaisant nuosekliai sujungtų varžinių komponentų skaičiaus, grandinės atkarpoje tekanti srovė nekeičia vertės.

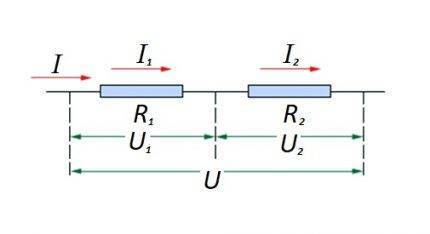Varžinių elementų sujungimas grandinės skyriuje nuosekliai vienas su kitu. Ši parinktis turi savo skaičiavimo įstatymą. Diagramoje: I, I1, I2 - srovės srautas; R1, R2 - varžiniai elementai; U, U1, U2 - taikoma įtampa

Įtampa, taikoma grandinės aktyviosioms varžinėms sudedamosioms dalims, yra suma ir pridedama prie EML šaltinio vertės.

Šiuo atveju kiekvieno atskiro komponento įtampa yra: Ux = I * Rx.

Bendra varža turėtų būti laikoma visų grandinės varžinių komponentų verčių suma.

Lygiagrečiai sujungtų varžinių elementų grandinė

Tuo atveju, kai yra lygiagretus varžinių komponentų ryšys, formuluotė laikoma teisinga, atsižvelgiant į vokiečių fiziko Ohmo įstatymą:

• aš = aš₁ + aš₂ … ;
• U = U₁ = U₂ … ;
• 1/R = 1/R₁ + 1 / R₂ + …

Neatmetama galimybė sudaryti „mišraus“ grandinės dalis, kai naudojamos lygiagrečios ir nuoseklios jungtys.

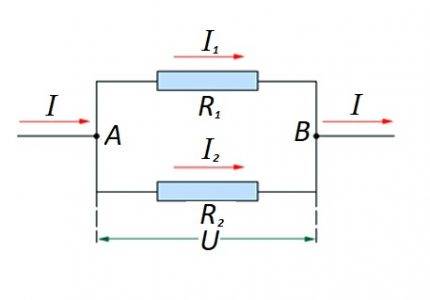Varžinių elementų sujungimas grandinės skyriuje lygiagrečiai vienas su kitu. Šiam variantui taikomas jo paties skaičiavimo įstatymas. Diagramoje: I, I1, I2 - srovės srautas; R1, R2 - varžiniai elementai; U - taikoma įtampa; A, B – įėjimo/išėjimo taškai

Tokių variantų atveju apskaičiavimas paprastai atliekamas iš pradžių apskaičiuojant lygiagrečios jungties varžą. Tada prie rezultato pridedama nuosekliai sujungto rezistoriaus vertė.

Integralios ir diferencinės teisės formos

Visi aukščiau pateikti taškai su skaičiavimais yra taikomi sąlygomis, kai, taip sakant, „homogeniškos“ struktūros laidininkai naudojami kaip elektros grandinių dalis.

Tuo tarpu praktikoje dažnai tenka susidurti su schemos konstravimu, kur įvairiose srityse keičiasi laidininkų struktūra. Pavyzdžiui, naudojami didesnio skerspjūvio laidai arba, atvirkščiai, mažesni, pagaminti iš skirtingų medžiagų.

Siekiant atsižvelgti į tokius skirtumus, yra vadinamasis „diferencialinis-integralus Ohmo įstatymas“. Be galo mažam laidininkui srovės tankio lygis apskaičiuojamas priklausomai nuo intensyvumo ir laidumo vertės.

Skaičiuojant skirtumą, imama formulė: J = ό * E

Atitinkamai integralui apskaičiuoti formulė: I * R = φ1 - φ2 + έ

Tačiau šie pavyzdžiai yra artimesni aukštosios matematikos mokyklai ir iš tikrųjų nėra naudojami tikroje paprasto elektriko praktikoje.

Srovės ir varžos supratimas

Pradėkime nuo elektros srovės sąvokos. Trumpai tariant, elektros srovė metalų atžvilgiu yra nukreiptas elektronų – neigiamai įkrautų dalelių – judėjimas. Paprastai jie vaizduojami kaip maži apskritimai.Ramioje būsenoje jie juda atsitiktinai, nuolat keisdami kryptį. Tam tikromis sąlygomis – atsiradus potencialų skirtumui – šios dalelės pradeda tam tikrą judėjimą tam tikra kryptimi. Šis judėjimas yra elektros srovė.

Kad būtų aiškiau, galime palyginti elektronus su vandeniu, išsiliejusiu kokioje nors plokštumoje. Kol lėktuvas stovi, vanduo nejuda. Bet, kai tik atsirado nuolydis (atsirado potencialų skirtumas), vanduo pradėjo judėti. Tas pats ir su elektronais.

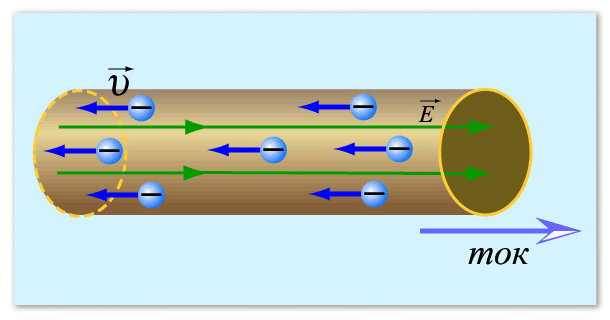
Taip galima įsivaizduoti elektros srovę

Dabar turime suprasti, kas yra pasipriešinimas ir kodėl jie turi grįžtamąjį ryšį su srovės stiprumu: kuo didesnis pasipriešinimas, tuo mažesnė srovė. Kaip žinote, elektronai juda laidininku. Paprastai tai yra metaliniai laidai, nes metalai gerai praleidžia elektrą. Žinome, kad metalas turi tankią kristalinę gardelę: daug dalelių, kurios yra artimos ir tarpusavyje susijusios. Elektronai, prasiskverbdami tarp metalo atomų, susiduria su jais, todėl jiems sunku judėti. Tai padeda iliustruoti laidininko pasipriešinimą. Dabar tampa aišku, kodėl kuo didesnė varža, tuo mažesnė srovės stipris – kuo daugiau dalelių, tuo elektronams sunkiau įveikti kelią, jie tai daro lėčiau. Atrodo, kad tai buvo sutvarkyta.

Jei norite empiriškai patikrinti šią priklausomybę, susiraskite kintamąjį rezistorių, nuosekliai sujunkite rezistorių - ampermetrą - srovės šaltinį (bateriją). Taip pat pageidautina į grandinę įkišti jungiklį - įprastą perjungimo jungiklį.

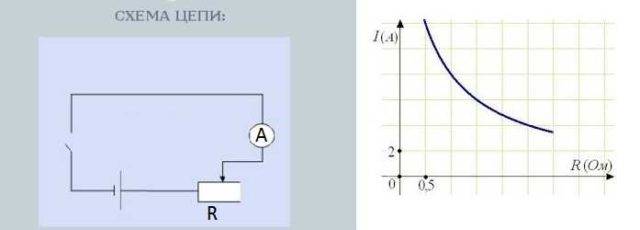
Grandinė, skirta patikrinti srovės priklausomybę nuo varžos

Sukant rezistoriaus rankenėlę keičiasi varža.Tuo pačiu metu keičiasi ir ampermetro, kuris matuoja srovės stiprumą, rodmenys. Be to, kuo didesnis pasipriešinimas, tuo mažiau rodyklė nukrypsta - tuo mažesnė srovė. Kuo mažesnė varža, tuo labiau rodyklė nukrypsta – srovė didesnė.

Srovės priklausomybė nuo varžos yra beveik tiesinė, tai yra, ji atsispindi grafike kaip beveik tiesi linija. Kodėl beveik – apie tai reikėtų kalbėti atskirai, bet tai jau kita istorija.

Omo dėsnis kintamajai srovei

Skaičiuojant kintamosios srovės grandines, vietoj varžos sąvokos įvedama „impedanso“ sąvoka. Varža žymima raide Z, ji apima aktyviąją apkrovos R varžą_a ir reaktyvumas X (arba R_r). Taip yra dėl sinusinės srovės (ir bet kokių kitų formų srovių) formos ir indukcinių elementų parametrų bei perjungimo dėsnių:

1. Srovė indukcinėje grandinėje negali akimirksniu pasikeisti.
2. Įtampa grandinėje su talpa negali pasikeisti akimirksniu.

Taigi, srovė pradeda atsilikti arba nukreipti įtampą, o tariama galia skirstoma į aktyviąją ir reaktyviąją.

U=I/Z

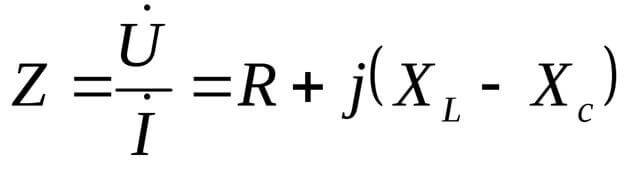
X_L ir X_C yra reaktyvieji apkrovos komponentai.

Šiuo atžvilgiu įvedama vertė cosФ:

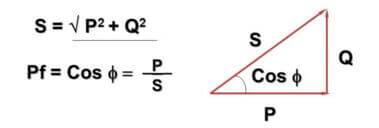
Čia - Q - reaktyvioji galia dėl kintamosios srovės ir indukcinių-talpinių komponentų, P - aktyvioji galia (išsklaidyta aktyviuosiuose komponentuose), S - tariama galia, cosФ - galios koeficientas.

Galbūt pastebėjote, kad formulė ir jos vaizdavimas kertasi su Pitagoro teorema. Tai tiesa ir kampas Ф priklauso nuo to, kokio dydžio yra apkrovos reaktyvioji dedamoji – kuo ji didesnė, tuo didesnė. Praktiškai tai lemia tai, kad tinkle faktiškai tekanti srovė yra didesnė, nei atsižvelgiama į buitinį skaitiklį, o įmonės moka už visą galią.

Šiuo atveju pasipriešinimas pateikiamas sudėtinga forma:

Čia j yra įsivaizduojamas vienetas, būdingas sudėtingai lygčių formai. Rečiau vadinama i, tačiau elektrotechnikoje žymima ir efektyvioji kintamosios srovės vertė, todėl, kad nesusipainiotume, geriau naudoti j.

Įsivaizduojamas vienetas yra √-1. Logiška, kad kvadratuojant tokio skaičiaus nėra, dėl kurio gali būti gautas neigiamas rezultatas „-1“.

Kai atsiranda Omo dėsnis

Sukurti idealias sąlygas nėra lengva. Net grynuose laidininkuose elektrinė varža kinta priklausomai nuo temperatūros. Jo sumažėjimas sumažina kristalinės gardelės molekulių aktyvumą, o tai supaprastina laisvųjų krūvių judėjimą. Esant tam tikram „užšalimo“ lygiui, atsiranda superlaidumo efektas. Šildant pastebimas priešingas efektas (laidumo pablogėjimas).

Tuo pačiu metu elektrolitai, metalai ir tam tikros keramikos rūšys išlaiko elektrinę varžą nepriklausomai nuo srovės tankio. Parametrų stabilumas išlaikant tam tikrą temperatūros režimą leidžia pritaikyti Ohmo dėsnio formules be papildomų pataisymų.

Puslaidininkinės medžiagos ir dujos pasižymi skirtinga elektrine varža. Šiam parametrui didelę įtaką turi srovės intensyvumas valdymo tūryje. Norint apskaičiuoti eksploatacines charakteristikas, reikia taikyti specializuotus skaičiavimo metodus.

Jei atsižvelgiama į kintamąją srovę, skaičiavimo metodas koreguojamas. Tokiu atveju reikės atsižvelgti į reaktyvių komponentų buvimą. Esant varžos pobūdžiui, galima taikyti svarstytas skaičiavimo technologijas remiantis Omo dėsnio formulėmis.

Kirchhoffo dėsniai.

Paskirstymas
srovės elektros grandinės atšakose
paklūsta pirmajam Kirchhoffo dėsniui,
ir įtempių pasiskirstymas per ruožus
grandinė paklūsta antrajam Kirchhoffo dėsniui.

Kirchhoffo dėsniai
kartu su Omo dėsniu yra pagrindiniai
elektros grandinių teorijoje.

Pirmas
Kirchhoffo dėsnis:

Algebrinė
srovių suma mazge lygi nuliui:

_i
= 0 (19)

Kur
i
yra šakų, susiliejančių tam tikrame mazge, skaičius.

Tai yra, sumavimas
tęsiasi iki srovių šakose,
kurios susilieja į svarstomą
mazgas.

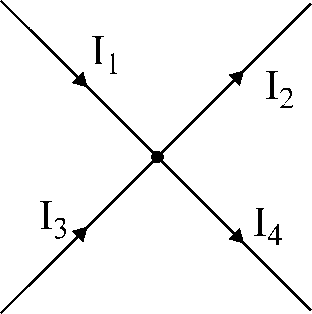
17 pav. Iliustracija
pagal pirmąjį Kirchhoffo dėsnį.

Skaičius
lygtys sudarytos pagal pirmąją
Kirchhoffo dėsnis nustatomas pagal formulę:

Nup
= Nu
– 1,

Kur
Nu
yra mazgų skaičius nagrinėjamoje grandinėje.

Srovių požymiai
lygtys imamos atsižvelgiant į pasirinktą
teigiama kryptimi. Ženklai adresu
srovės yra vienodos, jei srovės yra vienodos
orientuota į tai
mazgas.

Pavyzdžiui,
17 pav. parodytam mazgui:
į mazgą tekančioms srovėms priskiriame ženklus
„+“, o į sroves, ištekančias iš mazgo – ženklai
«-».

Tada lygtis
pagal pirmąjį Kirchhoffo dėsnį bus parašyta
Taigi:

aš₁
– aš₂
+ aš₃
– aš₄
= 0.

lygtys,
sudarytas pagal pirmąjį Kirchhoffo dėsnį,
vadinami mazgais.

Tai
įstatymas išreiškia tai, kad mazge
elektros krūvis nesikaupia
ir nėra vartojamas. Elektros kiekis
į svetainę ateinantys mokesčiai yra lygūs sumai
krūviai palieka mazgą viename ir tame pačiame
tą patį laiko tarpą.

Antra
Kirchhoffo dėsnis:

Algebrinė
emf suma bet kurioje uždaroje grandinėje
grandinė lygi algebrinei kritimų sumai
šios grandinės elementų įtampa:

Ui
= 
Ei

IiRi=Ei(20)

Kur
i
- elemento numeris (varža arba
įtampos šaltinis) svarstomoje
kontūras.

**Skaičius
lygtys sudarytos pagal antrą
Kirchhoffo dėsnis nustatomas pagal formulę:

Nup
= Nb
-Nu
+ 1 – Ned.s.

Kur
Nb
- elektros grandinės šakų skaičius;

Nu
— mazgų skaičius;

Ned.s.
yra idealių emf šaltinių skaičius.

18 pav. Iliustracija
pagal antrąjį Kirchhoffo dėsnį.

Dėl,
teisingai parašyti antrąjį dėsnį
Kirchhoff, esant tam tikram kontūrui, toliau
laikytis šių taisyklių:

1. savavališkai
   pasirinkite kontūro apėjimo kryptį,
   pavyzdžiui, pagal laikrodžio rodyklę (18 pav.).

2. emf
   ir atitinkantys įtampos kritimus
   kryptimi su pasirinkta kryptimi
   apeiti yra parašyti išraiškoje su
   ženklas „+“; jei e.f.s. ir įtampos kritimas
   nesutampa kryptis
   kontūras, tada prieš juos rašomas ženklas
   «-».

Pavyzdžiui,
18 pav. kontūrui, antrasis Kirchhoffo dėsnis
bus parašyta taip:

U₁
– U₂
+ U₃
=E₁
– E₃
– E₄
(21)

(20) lygtis gali būti
perrašyti kaip:

 (Ui
– Ei)
= 0 (22)

Kur
(U
– E)
- įtampa ant šakos.

Vadinasi,
Galima suformuluoti antrąjį Kirchhoffo dėsnį
tokiu būdu:

Algebrinė
šakose esančių įtampų suma bet kurioje
uždara kilpa yra nulis.

Potencialus
anksčiau aptarta diagrama
grafinė antrojo interpretacija
Kirchhoffo dėsnis.

Užduotis numeris 1.

AT
1 pav. pavaizduotai grandinei pateiktos srovės I₁
ir aš₃,
pasipriešinimas ir emf Nustatyti sroves
aš₄,
aš₅,
aš₆
; įtampa tarp taškų a
ir b
jeigu aš₁
= 10 mA,
aš₃
= -20 mA,
R₄
= 5 kOhm,
E₅
= 20 mlrd.,
R₅
= 3 kOhm,
E₆
= 40B,
R₆
= 2 kOhm.

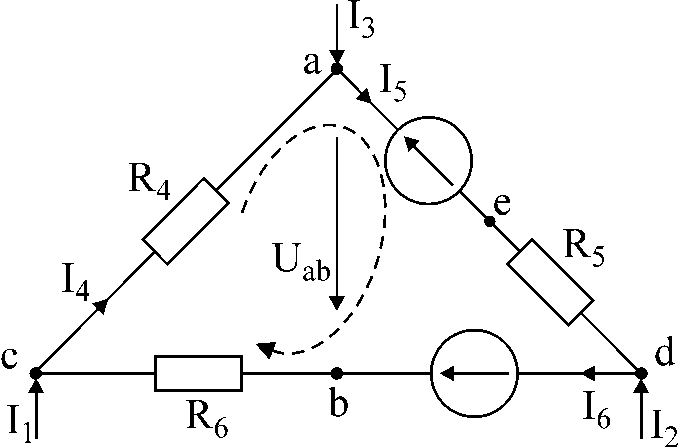
1 pav

Sprendimas:

1. Už duotybę
   kontūrą, sudarome dvi lygtis pagal
   Pirmasis Kirchhoffo dėsnis ir vienas – pagal
   antra. Kontūro kryptis
   nurodyta rodykle.

AT
kaip sprendinį gauname: I₆
= 0; aš₄
= 10 mA;
aš₅
= -10 mA

1. paklausti
   įtampos kryptis tarp taškų
   a
   ir b
   iš taško "a"
   į tašką "b"
   – U_ab.
   Šią įtampą galima rasti iš lygties
   Antrasis Kirchhoffo dėsnis:

aš₄R₄
+ U_ab
+ aš₆R₆
= 0

U_ab
= - 50V.

Užduotis numeris 2.

Dėl
diagramos 2 pav. sudaryti lygtis pagal
Kirchhoffo dėsnius ir nustato nežinomuosius
taškų.

Duota:
aš₁
= 20mA;
aš₂
= 10 mA

R₁
= 5 kOhm,
R₃
= 4 kOhm,
R₄
= 6 kOhm,
R₅
= 2 kOhm,
R₆
= 4kΩ.

2 pav

Sprendimas:

Mazgų skaičius
lygtys - 3, kontūrinių lygčių skaičius
– 1.

Prisiminti!
Sudarant lygtį pagal antrą
Kirchhoffo dėsnis, pasirenkame kontūrą, in
kuri neapima dabartinių šaltinių.
Kontūro kryptis nurodyta paveikslėlyje.

AT
šios grandinės šakų I srovės₁
ir aš₂.
Nežinoma
srovės
aš₃,
aš₄,
aš₅,
aš₆.

Sprendžiant
sistemą, gauname: I₃
= 13,75 mA;
aš₄
= -3,75 mA;
aš₅
= 6,25 mA;
aš₆
= 16,25 mA.

Pagrindinės sąvokos

Elektros srovė teka, kai uždara grandinė leidžia elektronams pereiti iš didelio potencialo į žemesnį grandinėje. Kitaip tariant, srovei reikalingas elektronų šaltinis, turintis energijos jiems pajudinti, taip pat neigiamų krūvių sugrįžimo taškas, kuriam būdingas jų trūkumas. Kaip fizinis reiškinys, srovė grandinėje apibūdinama trimis pagrindiniais dydžiais:

• Įtampa;
• srovės stiprumas;
• laidininko, kuriuo juda elektronai, varža.

Jėga ir įtampa

Srovės stipris (I, matuojamas amperais) yra elektronų (krūvio) tūris, judantis tam tikra grandinės vieta per laiko vienetą. Kitaip tariant, I matavimas yra judančių elektronų skaičiaus nustatymas

Svarbu suprasti, kad šis terminas reiškia tik judėjimą: statiniai krūviai, pavyzdžiui, ant neprijungto akumuliatoriaus gnybtų, neturi išmatuojamos vertės I. Srovė, kuri teka viena kryptimi, vadinama tiesiogine (DC), o periodiškai besikeičianti kryptis vadinama kintamąja (AC). Įtampa gali būti iliustruojama tokiu reiškiniu kaip slėgis arba kaip gravitacijos veikiamų objektų potencinės energijos skirtumas

Norėdami sukurti šį disbalansą, pirmiausia turite eikvoti energiją, kuri bus realizuota judant atitinkamomis aplinkybėmis. Pavyzdžiui, nukritus kroviniui iš aukščio, atliekami darbai jį pakelti, galvaninėse baterijose potencialų skirtumas gnybtuose susidaro dėl cheminės energijos konversijos, generatoriuose - dėl poveikio elektromagnetinis laukas

Stresą galima iliustruoti tokiu reiškiniu kaip slėgis arba kaip gravitacijos veikiamų objektų potencialios energijos skirtumas. Norėdami sukurti šį disbalansą, pirmiausia turite eikvoti energiją, kuri bus realizuota judant atitinkamomis aplinkybėmis. Pavyzdžiui, nukritus kroviniui iš aukščio, realizuojamas jo kėlimo darbas, galvaniniuose akumuliatoriuose potencialų skirtumas gnybtuose susidaro dėl cheminės energijos konversijos, generatoriuose - dėl poveikio elektromagnetinis laukas.

Laidininko varža

Kad ir koks geras būtų paprastas laidininkas, jis niekada neleis elektronams praeiti be tam tikro pasipriešinimo jų judėjimui. Atsparumą galima laikyti mechaninės trinties analogu, nors šis palyginimas nebus tobulas.Kai srovė teka laidininku, tam tikras potencialų skirtumas paverčiamas šiluma, todėl rezistoriuje visada bus įtampos kritimas. Elektriniai šildytuvai, plaukų džiovintuvai ir kiti panašūs prietaisai skirti tik elektros energijai išsklaidyti šilumos pavidalu.

Supaprastinta varža (žymima R) yra matas, nurodantis, kiek elektronų srautas sulėtėja grandinėje. Jis matuojamas omais. Rezistoriaus ar kito elemento laidumą lemia dvi savybės:

• geometrija;
• medžiaga.

Forma yra nepaprastai svarbi, kaip matyti iš hidraulinės analogijos: stumti vandenį per ilgą ir siaurą vamzdį yra daug sunkiau nei stumti vandenį per trumpą ir platų. Medžiagos vaidina lemiamą vaidmenį. Pavyzdžiui, elektronai gali laisvai judėti varinėje laidoje, bet negali tekėti per izoliatorius, tokius kaip guma, nepaisant jų formos. Be geometrijos ir medžiagos, yra ir kitų veiksnių, turinčių įtakos laidumui.

Omo dėsnio aiškinimas

Norėdami užtikrinti įkrovų judėjimą, turite uždaryti grandinę. Jei nėra papildomos galios, srovė negali egzistuoti ilgą laiką. Potencialai greitai taps lygūs. Norint išlaikyti grandinės veikimo režimą, reikalingas papildomas šaltinis (generatorius, baterija).

Visoje grandinėje bus bendra visų komponentų elektrinė varža. Norint atlikti tikslius skaičiavimus, atsižvelgiama į nuostolius laiduose, varžiniuose elementuose ir maitinimo šaltinyje.

Kiek įtampos reikia naudoti tam tikram srovės stiprumui, apskaičiuojama pagal formulę:

U=I*R.

Panašiai, pasitelkus nagrinėjamus ryšius, nustatomi ir kiti grandinės parametrai.

Lygiagretusis ir nuoseklusis ryšys

Elektrikoje elementai jungiami arba nuosekliai - vienas po kito, arba lygiagrečiai - tai yra tada, kai keli įėjimai yra prijungti prie vieno taško, o išėjimai iš tų pačių elementų prijungiami prie kito.

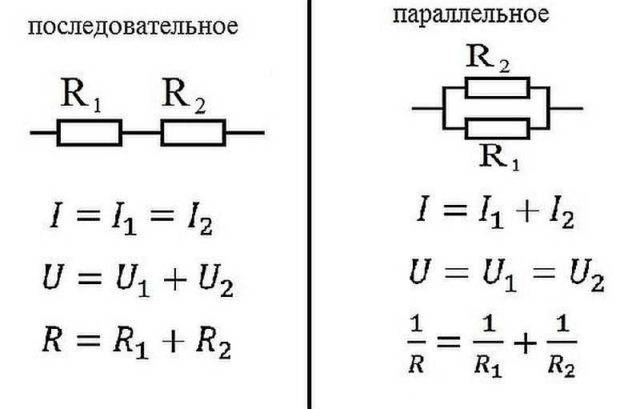
Lygiagrečio ir nuoseklaus ryšio Ohmo dėsnis

serijinis ryšys

Kaip Omo įstatymas veikia šiais atvejais? Sujungus nuosekliai, srovė, tekanti per elementų grandinę, bus tokia pati. Grandinės sekcijos su nuosekliai sujungtais elementais įtampa apskaičiuojama kaip kiekvienos sekcijos įtampų suma. Kaip tai galima paaiškinti? Srovės tekėjimas per elementą – tai dalies krūvio perkėlimas iš vienos jo dalies į kitą. Aš turiu galvoje, tai yra darbas. Šio darbo mastas – įtampa. Tai yra fizinė streso prasmė. Jei tai aišku, judame toliau.

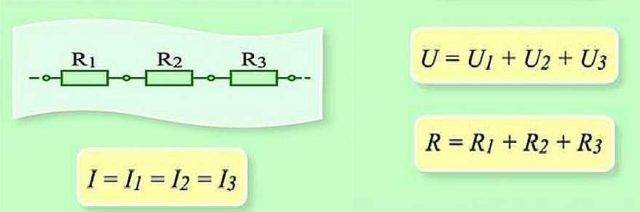
Nuoseklus ryšys ir šios grandinės sekcijos parametrai

Sujungus nuosekliai, įkrovą reikia perkelti paeiliui per kiekvieną elementą. Ir kiekvienam elementui tai yra tam tikras „darbo kiekis“. Ir norėdami sužinoti darbo kiekį visoje grandinės dalyje, turite pridėti kiekvieno elemento darbą. Taigi paaiškėja, kad bendra įtampa yra kiekvieno elemento įtampų suma.

Tokiu pat būdu - papildymo pagalba - randama ir bendra grandinės sekcijos varža. Kaip tu tai įsivaizduoji? Srovė, tekanti per elementų grandinę, nuosekliai įveikia visas varžas. Vienas po kito. Tai yra, norint rasti pasipriešinimą, kurį jis įveikė, reikia susumuoti pasipriešinimus. Daugiau ar mažiau taip. Matematinis išvedimas yra sudėtingesnis ir lengviau suprasti šio dėsnio mechanizmą.

Lygiagretus ryšys

Lygiagretusis ryšys yra tada, kai laidininkų / elementų pradžios viename taške susilieja, o kitame jų galai yra sujungti. Pabandysime paaiškinti dėsnius, kurie galioja tokio tipo junginiams. Pradėkime nuo srovės. Į elementų sujungimo tašką tiekiama tam tikro dydžio srovė. Jis atsiskiria, teka per visus laidininkus. Iš to darome išvadą, kad bendra srovė skyriuje yra lygi kiekvieno elemento srovės sumai: I = I1 + I2 + I3.

Dabar apie įtampą. Jei įtampa yra darbas norint perkelti įkrovą, tada darbas, kurio reikia norint perkelti vieną įkrovą, bus vienodas bet kuriame elemente. Tai yra, kiekvieno lygiagrečiai prijungto elemento įtampa bus vienoda. U=U1=U2=U3. Ne taip smagu ir vizualu, kaip Omo dėsnio paaiškinimo grandinės atkarpai atveju, bet jūs galite suprasti.

Lygiagretaus ryšio įstatymai

Dėl pasipriešinimo viskas yra šiek tiek sudėtingesnė. Supažindinkime su laidumo sąvoka. Tai charakteristika, rodanti, kaip lengva ar sunku įkrovimui praeiti per šį laidininką. Akivaizdu, kad kuo mažesnė varža, tuo lengviau praeis srovė. Todėl laidumas – G – apskaičiuojamas kaip varžos atvirkštinė vertė. Formulėje ji atrodo taip: G = 1/R.

Kodėl mes kalbame apie laidumą? Kadangi sekcijos su lygiagrečiai sujungtos elementų suminis laidumas yra lygus kiekvienos sekcijos laidumo sumai. G = G1 + G2 + G3 – lengva suprasti. Kaip lengvai srovė įveiks šį lygiagrečių elementų mazgą, priklauso nuo kiekvieno elemento laidumo. Taigi išeina, kad juos reikia sulankstyti.

Dabar galime pereiti prie pasipriešinimo. Kadangi laidumas yra varžos atvirkštinis dydis, galime gauti tokią formulę: 1/R = 1/R1 + 1/R2 + 1/R3.

Kas suteikia mums lygiagretųjį ir nuoseklųjį ryšį?

Teorinės žinios yra gerai, bet kaip jas pritaikyti praktiškai? Bet kokio tipo elementus galima jungti lygiagrečiai ir nuosekliai. Bet mes svarstėme tik paprasčiausias formules, apibūdinančias tiesinius elementus. Linijiniai elementai yra varžos, kurios dar vadinamos „rezistoriais“. Taigi, štai kaip galite panaudoti tai, ką išmokote:

Jei didelės vertės rezistorių nėra, o yra keli mažesni, norimą varžą galima gauti nuosekliai sujungus kelis rezistorius. Kaip matote, tai yra naudinga technika.
Norint prailginti baterijų tarnavimo laiką, jas galima jungti lygiagrečiai. Tokiu atveju įtampa pagal Ohmo dėsnį išliks tokia pati (įsitikinsite matuodami įtampą multimetru). Ir dvigubos baterijos „eksploatavimo laikas“ bus daug ilgesnis nei dviejų elementų, kurie pakeis vienas kitą

Tik atkreipkite dėmesį: lygiagrečiai galima jungti tik tokio paties potencialo maitinimo šaltinius. Tai reiškia, kad negalima prijungti mirusios ir naujos baterijos.

Jei vis tiek prijungsite, didesnio įkrovimo akumuliatorius bus linkęs įkrauti mažiau įkrautą. Dėl to jų bendras mokestis sumažės iki mažos vertės.

Apskritai šie junginiai dažniausiai naudojami.

Idealus EMF šaltinis

Elektrovaros jėga (E) – fizikinis dydis, nulemiantis išorinių jėgų įtakos judėjimui uždaroje krūvininkų grandinėje laipsnį. Kitaip tariant, kaip stipri srovė linkusi tekėti per laidininką, priklausys nuo EML.

Namų mokyklų mokytojai, aiškindami tokius nesuprantamus reiškinius, mėgsta kreiptis į hidraulinių analogijų metodą.Jei laidininkas yra vamzdis, o elektros srovė yra per jį tekančio vandens kiekis, tada EMF yra slėgis, kurį sukuria siurblys siurbiant skystį.

Terminas elektrovaros jėga yra susijęs su tokia sąvoka kaip įtampa. Ji, EMF, taip pat matuojama voltais (vienetas - "V"). Kiekvienas maitinimo šaltinis, ar tai būtų baterija, generatorius ar saulės baterija, turi savo elektrovaros jėgą. Dažnai šis EML yra artimas išėjimo įtampai (U), bet visada šiek tiek mažesnis už ją. Tai sukelia šaltinio vidinė varža, ant kurios neišvengiamai nukrenta dalis įtampos.

Dėl šios priežasties idealus EML šaltinis yra veikiau abstrakti sąvoka arba fizinis modelis, kuriam nėra vietos realiame pasaulyje, nes akumuliatoriaus vidinė varža Rin, nors ir labai maža, vis tiek skiriasi nuo absoliutaus nulio.

Idealus ir tikras emf šaltinis

Diferencialinėje formoje

Formulė labai dažnai pateikiama diferencine forma, nes laidininkas dažniausiai yra nehomogeniškas ir jį reikės suskaidyti į kuo mažesnes dalis. Per ją einanti srovė yra susijusi su dydžiu ir kryptimi, todėl ji laikoma skaliariniu dydžiu. Kai reikia rasti gaunamą srovę per laidą, imama visų atskirų srovių algebrinė suma. Kadangi ši taisyklė taikoma tik skaliariniams dydžiams, srovė taip pat laikoma skaliariniu kiekiu. Yra žinoma, kad srovė dI = jdS eina per atkarpą. Įtampa ant jo yra lygi Edl, tada pastovaus skerspjūvio ir vienodo ilgio laidui santykis bus teisingas:

Diferencinė forma

Todėl srovės išraiška vektorine forma bus tokia: j = E.

Svarbu! Metalinių laidininkų atveju, kylant temperatūrai, laidumas mažėja, o puslaidininkių jis didėja. Omovo įstatymas neparodo griežto proporcingumo

Didelės grupės metalų ir lydinių atsparumas išnyksta esant temperatūrai, artimai absoliučiam nuliui, ir šis procesas vadinamas superlaidumu.